本文的代码参数以Kyber256参数为例,简述了NTT、T-NTT、Pt-NTT等算法的实现思路与特征
NTT
我们在本小节首先给出标准NTT算法的实现
Lemma
对于$\mathcal{R}_q=\mathbb{Z}_q[x]/(x^n+1)$,如果$2n|q-1$,则有$\zeta\in\mathbb{Z}_q[x]$,满足$ord(\zeta)=2n$,即$\zeta^{2n}\equiv 1~~mod~q$,且$k<2n$时$\zeta^{k}\not\equiv 1$
NTT Algorithm
对于$f\in\mathcal{R_q}$,定义$f=(f_0,f_1,\cdots,f_{n-1})$,$NTT(f)=(f(\zeta),f(\zeta^{3}),\cdots,f(\zeta^{2n-1}))$,n is power of 2,于是利用矩阵写出点值表示为:
$$\begin{pmatrix}\zeta^{0} & \zeta^{1} & \zeta^{2} & \cdots & \zeta^{n-1} \cr\zeta^{3\times 0} & \zeta^{3\times 1} & \zeta^{3\times 2} & \cdots & \zeta^{3\times (n-1)} \cr\vdots & \vdots & \vdots & \ddots & \vdots\cr\zeta^{(2n-1)\times 0} & \zeta^{(2n-1)\times 1} & \zeta^{(2n-1)\times 2} & \cdots & \zeta^{(2n-1)\times (n-1)} \cr\end{pmatrix}\begin{pmatrix}f_{0} \cr f_{1} \cr\vdots \cr f_{n-1}\end{pmatrix}=\begin{pmatrix}\hat{f_{0}} \cr\hat{f_{1}} \cr\vdots \cr\hat{f_{n-1}}\end{pmatrix}$$
其中
$$\begin{equation*}\begin{aligned}\hat{f_{j}}&=\sum_{i=0}^{n-1}f_{i}\cdot\zeta^{(2j+1)\cdot i}\cr&=\sum_{i=0}^{n-1}(f_{i}\cdot\zeta^{i})\cdot\omega^{j\cdot i}~~~~(\omega\equiv\zeta^2~~mod~q)\end{aligned}\end{equation*}$$
于是上述矩阵可另写作:
$$\begin{pmatrix}\omega^{0\times 0} & \omega^{0\times 1} & \omega^{0\times 2} & \cdots & \omega^{0\times (n-1)} \cr\omega^{1\times 0} & \omega^{1\times 1} & \omega^{1\times 2} & \cdots & \omega^{1\times (n-1)} \cr\vdots & \vdots & \vdots & \ddots & \vdots\cr\omega^{(n-1)\times 0} & \omega^{(n-1)\times 1} & \omega^{(n-1)\times 2} & \cdots & \omega^{(n-1)\times (n-1)} \cr\end{pmatrix}\begin{pmatrix}\zeta^{0} & & & & \cr& \zeta^{1} & & & \cr& & \zeta^{2} & & \cr& & & \ddots & \cr& & & & \zeta^{(n-1)} \cr\end{pmatrix}\begin{pmatrix}f_{0} \cr f_{1} \cr\vdots \cr f_{n-1}\end{pmatrix}=\begin{pmatrix}\hat{f_{0}} \cr\hat{f_{1}} \cr\vdots \cr\hat{f_{n-1}}\end{pmatrix}$$
中国剩余定理(CRT)给出了一种同构关系,我们可以通过下面的树形结构优化时间复杂度: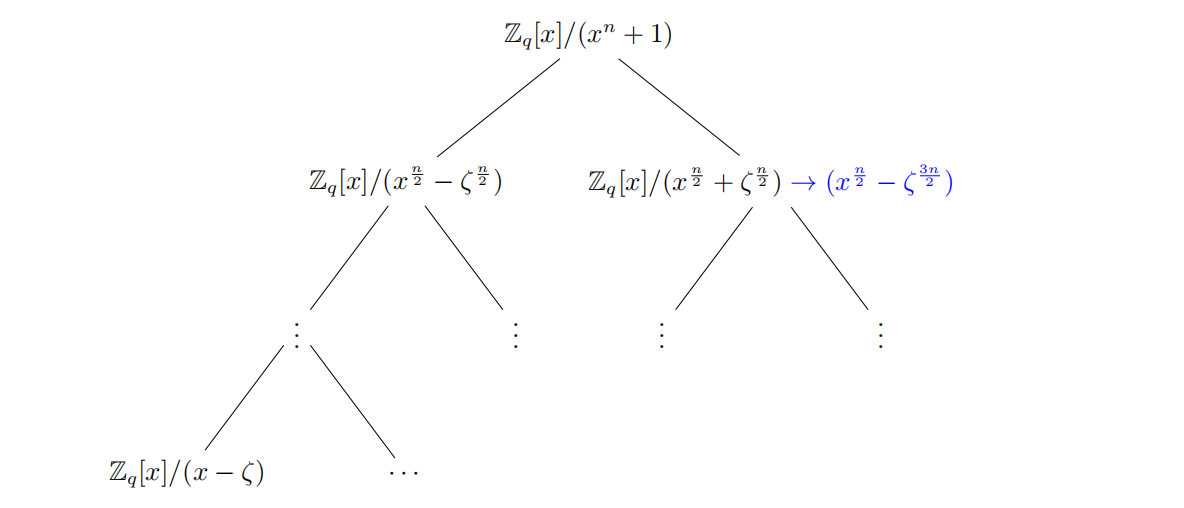
对于最后一层第$i$个叶子节点,其形式为$\mathbb{Z}_q[x]/(x-\zeta^{2br(i)+1})$,$br(i)$是$i$的比特翻转结果
void poly_ntt(uint16_t* r, int dim)
{
uint16_t m, i, j, j_1, V, t, U, j_2;
t = dim;
//printf("test:\n");
for (m = 1; m < dim; m = 2 * m)
{
t = t / 2;
//printf("\n%d:\n", t);
for (i = 0; i < m; i++)
{
j_1 = 2 * i * t;
j_2 = j_1 + t - 1;
for (j = j_1; j <= j_2; j++)
{
U = r[j] % Q;
V = r[j + t] * phi[m + i] % Q;
r[j] = (U + V) % Q;
r[j + t] = (U - V + 4 * Q) % Q;
}
}
/*printf("\n");
for (int index = 0; index < dim; index++) {
printf("%d,",r[index]);
}*/
}
// poly_bitrev(r);
}
T-NTT
有时未必会找到可以彻底分解的$n$,例如当$2n>q$时会出现分解不完全的情况(Kyber256方案中$n=256$,$q=3329$便仅满足$n|q-1$),考虑$\mathbb{Z_{17}}[x]/(x^{16}+1)$,利用第一节的思路我们可以得到: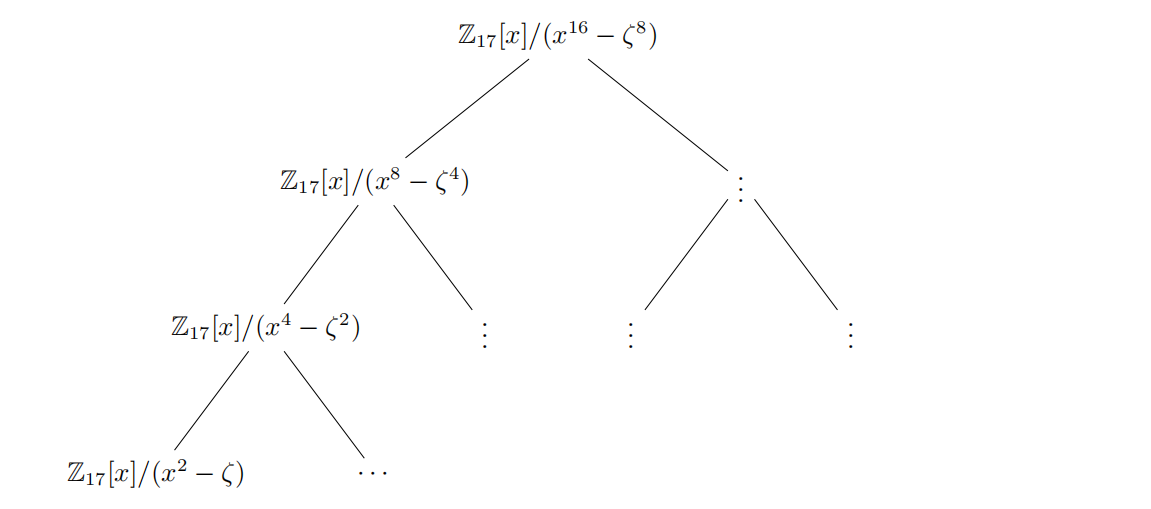
对于此种不完全分解的情况,以叶子节点$\mathbb{Z_{17}}[x]/(x^{2}-\zeta)$为例,多项式$f$和$g$此时可写作$\hat{f_{0}}+\hat{f_{1}}\cdot x$,$\hat{g_{0}}+\hat{g_{1}}\cdot x$,得到乘积多项式$\hat{f_{0}}\cdot\hat{g_{0}}+\hat{f_{1}}\cdot\hat{g_{1}}\zeta+(\hat{f_{0}}\cdot\hat{g_{1}}+\hat{f_{1}}\cdot\hat{g_{0}})x$,于是$$\hat{h_{0}}=\hat{f_{0}}\cdot\hat{g_{0}}+\hat{f_{1}}\cdot\hat{g_{1}}\zeta$$ $$\hat{h_{1}}=\hat{f_{0}}\cdot\hat{g_{1}}+\hat{f_{1}}\cdot\hat{g_{0}}$$
因此将T-NTT算法表示为$T-NTT(f)=(\hat{f_{0}}+\hat{f_{1}}\cdot x,\hat{f_{2}}+\hat{f_{3}}\cdot x,\cdots,\hat{f_{n-2}}+\hat{f_{n-1}}\cdot x)$
Pt-NTT
依旧针对T-NTT小节提出的例子,Pt-NTT算法采用了分治的思想处理
Lemma
Karatsuba算法指出在计算$(a_{0}+a_{1}\cdot x)\cdot (b_{0}+b_{1}\cdot x)$时,我们可以通过计算$a_{0}\cdot b_{0}+a_{1}\cdot b_{1}\cdot x^{2}+[(a_{0}+a_{1})\cdot(b_{0}+b_{1})-a_{0}\cdot b_{0}-a_{1}\cdot b_{1}]\cdot x$得到,减少一次大数乘法运算
Pt-NTT Algorithm
在Pt-NTT算法中($\alpha=1$),我们将多项式$f$写作$f=f_{o}(x^{2})+f_{e}(x^{2})\cdot x$,令$y=x^{2}$得到,$f=f_{o}(y)+f_{e}(y)\cdot x$
利用Karatsuba算法得到
$$\begin{equation*}\begin{aligned}f\cdot g &=f_{o}(y)\cdot g_{o}(y)+f_{e}(y)\cdot g_{e}(y)\cdot y+[f_{o}(y)\cdot g_{e}(y)+f_{e}(y)\cdot g_{o}(y)]\cdot x\cr&=h_{o}(y)\cdot h_{e}(y)\cdot x\end{aligned}\end{equation*}$$
于是我们将问题转到$\mathbb{Z_{17}}[y]/(y^{8}+1)$,可以通过NTT算法求解
对于一般形式的参数$\alpha$,我们将多项式$F$写作$F_{0}(y)+F_{1}(y)\cdot x+\cdots+F_{2^{\alpha}-1}(y)\cdot x^{2^{\alpha}-1}$
void poly_1ptntt(uint16_t* f, uint16_t* g, uint16_t* h, int dim, int inv_n)
{
uint16_t f_even[N / 2], f_odd[N / 2], g_even[N / 2], g_odd[N / 2], g_odd_1[N / 2], fg_even[N / 2], fg_odd[N / 2], fg_odd_1[N / 2], fg_eo[N / 2], fg_oe[N / 2], h_even[N / 2], h_odd[N / 2];
int i;
//f[dim]
for (i = 0; i < dim; i++)
{
f_even[i] = f[2 * i];
f_odd[i] = f[2 * i + 1];
g_even[i] = g[2 * i];
g_odd[i] = g[2 * i + 1];
}
for (i = 1; i < dim; i++)
g_odd_1[i] = g_odd[i - 1];
g_odd_1[0] = -g_odd[dim - 1] + Q;
poly_ntt(f_even, dim);
poly_ntt(g_even, dim);
poly_pointwise(f_even, g_even, fg_even, dim);
poly_ntt(g_odd_1, dim);
poly_ntt(f_odd, dim);
poly_pointwise(f_odd, g_odd_1, fg_odd_1, dim);
for (i = 0; i < dim; i++)
h_even[i] = (fg_even[i] + fg_odd_1[i]) % Q;
poly_invntt(h_even, dim, inv_n);
poly_pointwise(f_odd, g_even, fg_oe, dim);
poly_ntt(g_odd, dim);
poly_pointwise(f_even, g_odd, fg_eo, dim);
for (i = 0; i < dim; i++)
h_odd[i] = (fg_oe[i] + fg_eo[i]) % Q;
poly_invntt(h_odd, dim, inv_n);
for (i = 0; i < dim; i++)
{
h[2 * i] = h_even[i];
h[2 * i + 1] = h_odd[i];
}
}
void poly_1Iptntt_kara(uint16_t* f, uint16_t* g, uint16_t* h, int dim, int inv_n)
{
uint16_t f_even[N / 2], f_odd[N / 2], g_even[N / 2], g_odd[N / 2], fg_even[N / 2], fg_odd[N / 2], fg_odd_1[N / 2], fg_odd_2[N / 2], h_even[N / 2], h_odd[N / 2];
int i;
//uint16_t temp_1[N/2];
//uint16_t temp[N / 2] = { 3844, 3837, 7362, 319, 405, 7276, 4784, 2897, 1996, 5685, 6812, 869, 1633, 6048, 5881, 1800, 4781, 2900, 2063, 5618, 198, 7483, 6094, 1587, 7462, 219, 3501, 4180, 3188, 4493, 6801, 880, 6526, 1155, 5417, 2264, 4608, 3073, 3566, 4115, 1886, 5795, 2573, 5108, 6461, 1220, 2563, 5118, 4556, 3125, 2819, 4862, 3789, 3892, 1402, 6279, 3141, 4540, 4501, 3180, 257, 7424, 6203, 1478, 1003, 6678, 1853, 5828, 3041, 4640, 4837, 2844, 1408, 6273, 6637, 1044, 2722, 4959, 993, 6688, 2880, 4801, 4149, 3532, 6266, 1415, 1682, 5999, 3078, 4603, 2562, 5119, 648, 7033, 4582, 3099, 6974, 707, 2990, 4691, 2681, 5000, 1438, 6243, 3901, 3780, 6556, 1125, 417, 7264, 2593, 5088, 2044, 5637, 5729, 1952, 6090, 1591, 5653, 2028, 5833, 1848, 7131, 550, 1228, 6453, 1097, 6584 };
uint16_t temp[N / 2] = { 17, 3312, 2761, 568, 583, 2746, 2649, 680, 1637, 1692, 723, 2606, 2288, 1041, 1100, 2229, 1409, 1920, 2662, 667, 3281, 48, 233, 3096, 756, 2573, 2156, 1173, 3015, 314, 3050, 279, 1703, 1626, 1651, 1678, 2789, 540, 1789, 1540, 1847, 1482, 952, 2377, 1461, 1868, 2687, 642, 939, 2390, 2308, 1021, 2437, 892, 2388, 941, 733, 2596, 2337, 992, 268, 3061, 641, 2688, 1584, 1745, 2298, 1031, 2037, 1292, 3220, 109, 375, 2954, 2549, 780, 2090, 1239, 1645, 1684, 1063, 2266, 319, 3010, 2773, 556, 757, 2572, 2099, 1230, 561, 2768, 2466, 863, 2594, 735, 2804, 525, 1092, 2237, 403, 2926, 1026, 2303, 1143, 2186, 2150, 1179, 2775, 554, 886, 2443, 1722, 1607, 1212, 2117, 1874, 1455, 1029, 2300, 2110, 1219, 2935, 394, 885, 2444, 2154, 1175 };
uint16_t f_eo[N / 2], g_eo[N / 2], fg_eo[N / 2];
for (i = 0; i < dim; i++)
{
f_even[i] = f[2 * i];
f_odd[i] = f[2 * i + 1];
g_even[i] = g[2 * i];
g_odd[i] = g[2 * i + 1];
}
poly_ntt(f_even, dim);
poly_ntt(g_even, dim);
poly_pointwise(f_even, g_even, fg_even, dim);
poly_ntt(g_odd, dim);
poly_ntt(f_odd, dim);
poly_pointwise(f_odd, g_odd, fg_odd_1, dim);
poly_pointwise(temp, fg_odd_1, fg_odd_2, dim);
for (i = 0; i < dim; i++)
h_even[i] = (fg_even[i] + fg_odd_2[i]) % Q;
poly_invntt(h_even, dim, inv_n);
for (i = 0; i < dim; i++)
h_odd[i] = ((f_even[i] + f_odd[i]) * (g_even[i] + g_odd[i]) - fg_even[i] - fg_odd_1[i]) % Q;
poly_invntt(h_odd, dim, inv_n);
for (i = 0; i < dim; i++)
{
h[2 * i] = h_even[i];
h[2 * i + 1] = h_odd[i];
}
}
